
Activities
Click on ‘more’ to discover the many possibilities of “low threshold, high ceiling” tasks. These are sourced from NRICH, University of Cambridge. There is also commentary on integrating the Proficiencies.
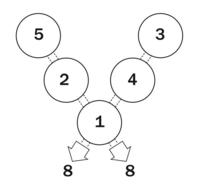
Activity: Magic Vs
Place each of the numbers from 1 to 5 in a V shape so that the two arms of the V have the same total sum.
Activity: Happy halving
Can you split various shapes in half so that the two parts are exactly the same?
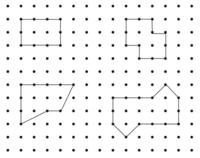
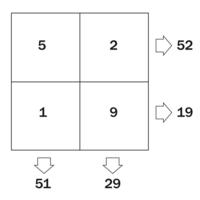
Activity: Reach 100
Your challenge is to place four different digits from 1 to 9 in a 2 x 2 grid that give four two-digit numbers which add to a total of 100.
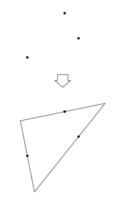
Activity: Triangle midpoints
Construct a triangle from its three midpoints.
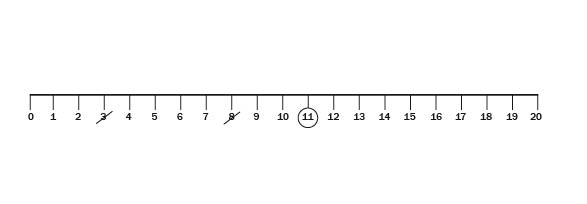
Activity: Strike it out
A game that involves calculations from crossing out numbers on a number line from 0 to 20.
Linking it all together
Paper by Lynne McClure (former director of NRICH) on ‘low threshold, high ceiling tasks’, published 2015 in Mathematics: Learn, Lead, Link (Proceedings of the 25th Biennial Conference of the Australian Association of Mathematics Teachers Inc.).
The birthday paradox
How many people do you need to have in a room for there to be a 50% chance of two people with a birthday on the same day (but not necessarily the same year)? How many to have a 99% probability of a match?
There only needs to be 23 people in a room for there to be a 50% chance of a shared birthday and only 57 people for there to be a 99% chance! Surprised?
Test it out by doing birthday surveys in your school. How many people before you get a match?
‘Proof’ that 2 = 1
let a = b, then a2 = ab
a2 – b2 = ab-b2
(a-b)(a+b) = b(a-b)
a+b = b, substituting gives b+b = b
2b = b therefore 2 = 1
Where is the error made?
Hilbert’s paradox of the Grand Hotel
The Grand Hotel has an infinite number of rooms, all of which are occupied. Can the hotel accommodate any more guests?
Does 0.999… = 1?
Sometimes this seems counter-intuitive. Try using fractions or algebra to show that this is true.
Zeno’s paradox
The finish line is 2 metres away. The runner must first reach half the distance to the finish line (1m) but when there must cover half of the remaining distance (1/2 m). Having done that the runner must cover half of the new remainder (1/4m), then 1/8m, then 1/16m etc.
Will the runner ever reach the finish line?
The potato paradox
You have 100kg of Martian potatoes, which are 99 percent water by weight. You let them dehydrate until they’re 98 percent water. How much do they weigh now?
A twist on Gardner’s two children problem
Mr Jones has two children. The older child is a girl. What is the probability that both children are girls?
Mr Smith has two children. At least one of them is a boy. What is the probability that both children are boys?
The twist:
Mr Ng has two children. One is a boy born on a Tuesday. What is the probability that both children are boys?
The Monty Hall problem
You are a contestant on a game show. At the show’s conclusion you are presented with three doors, each of which conceals a prize. Behind one of the doors is a car. Behind each of the other two doors is a goat.
After you have selected one of the doors, the host will open one of the two remaining doors to reveal a goat. At this point you will have the option of opening the door you originally selected and taking the prize behind it, or switching to the remaining unopened door and going home with the prize it conceals.
Is it in your best interest to switch? Will it improve your odds?
The missing square
Cut this triangle into pieces and reassemble it.
Why is there a missing square?
The two-envelope paradox
There are two envelopes, both containing money. One envelope has exactly twice the amount of money as the other. You can keep the money inside the envelope that you choose.
You pick one of the envelopes and open it. Inside is $20. Should you switch envelopes?
There are lots of activities based around two main themes.
Your place in the world relates to families (heritage, language spoken, time in Australia) and food (what we eat, how much, sources of food). The activities are developed from a personal perspective for the early years leading to the global for the secondary years.
About our world has a scientific focus, relating to weather and probability, and sustainability of food resources. The time frames start with a single day for the early years, progressing to weeks, months and years for primary students and then to hundreds of years for secondary classes.
Information and downloadable worksheets are broadly based. You are welcome to take and use ideas and activities that suit you and your students.
Early years activities
Your place in the world relates to families and food. The activities are developed from a personal perspective.
About our world relates to weather and probability. The time frames start with a single day.
Lower primary activities
Your place in the world relates to languages spoken in the home, and food sources. The activities are developed from a class and school perspective, moving into the local neighbourhood.
About our world relates to weather prediction around Australia, and the differences in weather, food and culture in the African country of Malawi.
Upper primary activities
Your place in the world relates to languages spoken in the home and family origins, and food choices. The activities are developed from a world perspective.
About our world relates to weather extremes around Australia, and the effect of climate change on the maize production in the African country of Malawi.
Junior secondary activities
Your place in the world relates to refugees and to agriculture. The activities are developed through an Australian then world perspective.
About our world looks at climate change. The time frames vary from years to decades.
Activities
Each cipher and code activity has a suggested level. However, many of the activities can be enjoyed by students (and teachers!) of all ages. Click on the links to download the activity sheets.
National Mathematics Day poster
Want to promote National Mathematics Day in your school? Print out this (PDF) poster and stick it up. (Formatted for A4 but can printed at any size.)
- Binary code nmd12_binary.pdf
- Braille nmd12_braille.pdf
- Caesar shift cipher nmd12_caesar_shift.pdf
- Dancing men cipher nmd12_dancing_men.pdf
- Frequency analysis nmd12_frequency.pdf
- Mary, Queen of Scots nmd12_mary_queen.pdf
- Pigpen cipher nmd12_pigpen.pdf
- Rail-fence cipher nmd12_rail-fence.pdf
- Scytale nmd12_scytale.pdf
- Semaphore nmd12_semaphore.pdf
- Sign language nmd12_sign_language.pdf
- International marine signal flags nmd12_marine_flags.pdf
- The Overland Telegraph line nmd12_overland_telegraph.pdf
About the SKA
Vastly more sensitive than the world’s best existing radio-telescopes, the Square Kilometre Array (SKA) will be one of the largest and most ambitious international science projects ever devised. It will help us answer fundamental questions about the evolution of the Universe.
Why the SKA on National Mathematics Day 2011?
National Mathematics Day is about celebrating mathematics, so in 2011, our theme is some of the mathematics in one of the great scientific adventures of our times.
Classroom activities
AAMT has collaborated with the staff at Questacon to bring you some classroom activities that will give your students some insights into the mathematics of the SKA and in astronomy more generally.


