Curricula

The senior secondary Australian Curriculum for Mathematics has been organised into four units, with the last two units designed to be cognitively more challenging than the first two. Each unit is designed to be taught in about half a ‘school year’ (approximately 50–60 hours duration including assessment and examinations). The units have also been designed so that they may be studied singly, in pairs over the course of a year, or as four units taken over two years.

State and territory curriculum authorities are responsible for the structure and organisation of the senior secondary curriculum implemented in their jurisdiction. They decide how the Australian Curriculum content and achievement standards are integrated into their courses. They continue to be responsible for assessment, certification and quality assurance in accordance with its respective legislation and the policy framework of its state government and Board (ACARA, 2020).

 

Essential Mathematics

• Seeks to prepare students for employment or further training.
• Focuses on using mathematics for problem solving and informed decision-making.

 

Unit 1	Unit 2	Unit 3	Unit 4
Calculations, percentages and rates Measurement Algebra Graphs	Representing and comparing data Percentages Rates and ratios Time and motion	Measurement Scales, plans and models Graphs Data collection	Probability and relative frequencies Earth geometry and time zones Loans and compound interest

 

General Mathematics

• Students explore a wide range of geometrical problems in areas such as measurement, scaling, triangulation and navigation.
• Focuses on problem-solving using discrete mathematics in contexts such as financial modelling, network analysis, route and project planning, decision making, and growth and decay.
• Provides opportunities for students to develop systematic strategies for answering statistical questions.

 

Unit 1	Unit 2	Unit 3	Unit 4
Consumer arithmetic Algebra and matrices Shape and measurement	Univariate data analysis and the statistical investigation process Applications of trigonometry Linear equations and their graphs	Bivariate data analysis Growth and decay in sequences Graphs and networks	Time series analysis Loans, investments and annuities Networks and decision mathematics

 

Mathematical Methods

• Focuses on developing understanding of the role of calculus, including the use of functions, their derivatives and integrals, in modelling physical processes.
• Students develop the ability to describe and analyse phenomena involving uncertainty and variation through their study of statistics.

 

Unit 1	Unit 2	Unit 3	Unit 4
Functions and graphs Trigonometric functions Counting and probability	Exponential functions Arithmetic and geometric sequences and series Introduction to differential calculus	Further differentiation and applications Integrals Discrete random variables	The logarithmic function Continuous random variables and the normal distribution Interval estimates for proportions

 

Specialist Mathematics

• Specialist Mathematics is taken in conjunction with, and builds on the study of functions and calculus in, Mathematical Methods.
• Provides opportunities to develop rigorous mathematical arguments and proofs and use mathematical models more extensively.
• Extends understanding of probability and statistics and introduces the topics of vectors, complex numbers and matrices.

 

Unit 1	Unit 2	Unit 3	Unit 4
Combinatorics Vectors in the plane Geometry	Trigonometry Matrices Real and complex numbers	Complex numbers Functions and sketching graphs Vectors in three dimensions	Integration and applications of integration Rates of change and differential equations Statistical inference

 

Source: https://www.australiancurriculum.edu.au/senior-secondary-curriculum/mathematics/

The senior secondary curriculum is managed by the Board of Senior Secondary Studies in the ACT.

Essential Mathematics

• Based on AC: Essential Mathematics.
• Focuses on using mathematics for problem solving and informed decision-making.

Mathematical Methods

• Based on AC: Mathematical Methods
• The discrete random variables and the logarithmic function topics have switched places between Units 3 and 4.

Specialist Mathematics

• Based on AC: Specialist Mathematics.

Mathematical Applications

• Based on AC: General Mathematics.

 

Source: http://www.bsss.act.edu.au/curriculum/australian_curriculum

Mathematics Standard 1 and 2

• A basic mathematics course containing precalculus concepts and heavily based on practical mathematics used in everyday life.

 

Mathematics Standard 1 Topics (Year 11)	Mathematics Standard 2 Topics (Year 12)
Algebra Formulae and Equations Linear Relationships Measurement Applications of Measurement Working with Time Financial Mathematics Money Matters Statistical Analysis Data Analysis Relative Frequency and Probability	Algebra Types of Relationships Linear Relationships Measurement Right-angled Triangles Rates Scale Drawings Financial Mathematics Investment Depreciation and Loans Statistical Analysis Further Statistical Analysis Networks Networks and Paths

Mathematics Advanced

• An advanced level calculus-based course with detailed study in probability and statistics, trigonometry, curve sketching, and applications of calculus. It is the highest level non-extension mathematics course.

 

Mathematics Advanced (Year 11)	Mathematics Advanced (Year 12)
Functions Working with Functions Trigonometric Functions Trigonometry and Measure of Angles Trigonometric Functions and Identities Calculus Introduction to Differentiation Exponential and Logarithmic Functions Logarithms and Exponentials Statistical Analysis Probability and Discrete Probability Distributions	Functions Graphing Techniques Trigonometric Functions Trigonometric Functions and Graphs Calculus Differential Calculus The Second Derivative ntegral Calculus Financial Mathematics Modelling Financial Situations Statistical Analysis Descriptive Statistics and Bivariate Data Analysis Random Variables

 

Mathematics Extension 1

• A more advanced course building on concepts in calculus, trigonometry, polynomials, basic combinatorics, vectors, and further statistics.
• Must be studied concurrently with Mathematics Advanced.

 

Mathematics Extension 1 (Year 11)	Mathematics Extension 1 (Year 12)
Functions Further Work with Functions Polynomials Trigonometric Functions Inverse Trigonometric Functions Further Trigonometric Identities Calculus Rates of Change Combinatorics Working with Combinatorics	Proof Proof by Mathematical Induction Vectors Introduction to Vectors Trigonometric Functions Trigonometric Equations Calculus Further Calculus Skills Applications of Calculus Statistical Analysis The Binomial Distribution

 

Mathematics Extension 2

• A highly advanced mathematics course containing an introduction to complex numbers, advanced calculus, motion, and further work with vectors.
• Must be studied concurrently with Mathematics Advanced & Mathematics Extension 1.

 

Mathematics Extension 2 (Year 12)

Proof The Nature of Proof Further Proof by Mathematical Induction Vectors Further Work with Vectors Complex Numbers Introduction to Complex Numbers Using Complex Numbers Calculus Further Integration Mechanics Applications of Calculus to Mechanics

 

 

Mathematics Life Skills

 

Mathematics Life Skills

Number and Modelling (Algebra) Review of Number Properties Mathematical Modelling Measurement Everyday Measurement Measuring Two-Dimensional and Three-Dimensional Shapes Financial Mathematics Decimals, Percentages and Money Earning Money Spending Money Statistics and Probability (Statistical Analysis) Statistics Probability Plans, Maps and Networks (Networks) Using Plans, Maps and Networks

 

Visit NSW Education Standards

 

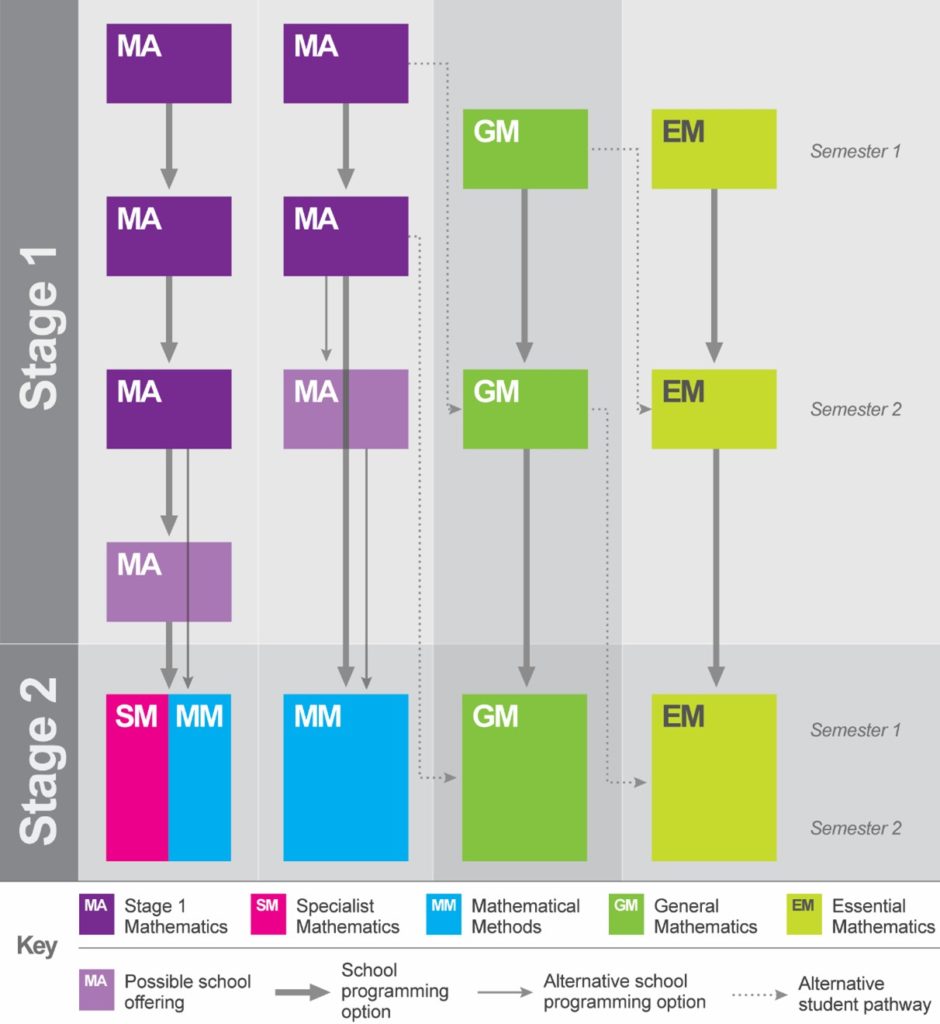
Mathematics (Stage 1)

• Provides a variety of contexts in algebra and geometry for incorporating mathematical arguments and problem-solving.

 

Topics 1 – 6	Topics 7 – 12
Functions and graphs Polynomials Trigonometry Counting and statistics Growth and decay Introduction to differential calculus	Arithmetic and geometric sequences and series  Geometry Vectors in the plane Further trigonometry Matrices Real and complex numbers.

 

• As a guide, Topics 1 to 6 prepare students for the study of Stage 2 Mathematical Methods and Topics 7 to 12 prepare students for the study of Stage 2 Specialist Mathematics.

 

General Mathematics (Stage 1 and 2)

• In Stage 1 students extend their mathematical skills through problem-solving and mathematical modelling in everyday contexts. There is an emphasis on consolidating computational and algebraic skills and expanding students’ ability to reason and analyse mathematically.
• In Stage 2 students develop a strong understanding of the process of mathematical modelling and its application to problem‑solving in everyday contexts.

 

Topics (Stage 1)	Topics (Stage 2)
Investing and borrowing Measurement Statistical investigation Applications of trigonometry Linear and exponential functions and their graphs Matrices and networks Open topic	Modelling with linear relationships Modelling with matrices Statistical models Financial models Discrete models Open topic Students study five topics from the list above. All students must study Topics 1, 3, 4, and 5.

 

Essential Mathematics (Stage 1 and 2)

• Essential Mathematics extends students’ mathematical skills in ways that apply to practical problem-solving in everyday and workplace contexts.
• In Stage 1 there is an emphasis on extending students’ computational skills and expanding their ability to apply their mathematical skills in flexible and resourceful ways.
• In Stage 2 a problem-based approach is used to develop mathematical skills and the associated key ideas.

 

Topics (Stage 1)	Topics (Stage 2)
Calculations, time, and ratio Earning and spending Geometry Data in context Measurement Investing Open topic	Scales, plans, and models Measurement Business applications Statistics Investments and loans Open topic Students study five topics from the list above. All students must study Topics 2, 4, and 5.

 

Mathematical Methods (Stage 2)

• Enables students to explore, describe, and explain aspects of the world around them by using calculus and statistics to model practical situations.

 

Topics (Stage 2)

Further differentiation and applications Discrete random variables Integral calculus Logarithmic functions Continuous random variables and the normal distribution Sampling and confidence intervals.

 

Specialist Mathematics (Stage 2)

• Extends students’ mathematical experience in the areas of complex numbers and vectors. The study of functions, differential equations, and dynamic systems provides opportunities to analyse the consequences of more complex laws of interaction.
• Specialist Mathematics provides different scenarios for incorporating mathematical arguments, proofs, and problem-solving.

 

Topics (Stage 2)

Mathematical induction Complex numbers Functions and sketching graphs Vectors in three dimensions Integration techniques and applications Rates of change and differential equations.

 

Mathematics (Stage 1)

• Provides a variety of contexts in algebra and geometry for incorporating mathematical arguments and problem-solving.

 

Topics 1 – 6	Topics 7 – 12
Functions and graphs Polynomials Trigonometry Counting and statistics Growth and decay Introduction to differential calculus	Arithmetic and geometric sequences and series  Geometry Vectors in the plane Further trigonometry Matrices Real and complex numbers.

 

• As a guide, Topics 1 to 6 prepare students for the study of Stage 2 Mathematical Methods and Topics 7 to 12 prepare students for the study of Stage 2 Specialist Mathematics.

 

General Mathematics (Stage 1 and 2)

• In Stage 1 students extend their mathematical skills through problem-solving and mathematical modelling in everyday contexts. There is an emphasis on consolidating computational and algebraic skills and expanding students’ ability to reason and analyse mathematically.
• In Stage 2 students develop a strong understanding of the process of mathematical modelling and its application to problem‑solving in everyday contexts.

 

Topics (Stage 1)	Topics (Stage 2)
Investing and borrowing Measurement Statistical investigation Applications of trigonometry Linear and exponential functions and their graphs Matrices and networks Open topic	Modelling with linear relationships Modelling with matrices Statistical models Financial models Discrete models Open topic Students study five topics from the list above. All students must study Topics 1, 3, 4, and 5.

 

Essential Mathematics (Stage 1 and 2)

• Essential Mathematics extends students’ mathematical skills in ways that apply to practical problem-solving in everyday and workplace contexts.
• In Stage 1 there is an emphasis on extending students’ computational skills and expanding their ability to apply their mathematical skills in flexible and resourceful ways.
• In Stage 2 a problem-based approach is used to develop mathematical skills and the associated key ideas.

 

Topics (Stage 1)	Topics (Stage 2)
Calculations, time, and ratio Earning and spending Geometry Data in context Measurement Investing Open topic	Scales, plans, and models Measurement Business applications Statistics Investments and loans Open topic Students study five topics from the list above. All students must study Topics 2, 4, and 5.

 

Mathematical Methods (Stage 2)

• Enables students to explore, describe, and explain aspects of the world around them by using calculus and statistics to model practical situations.

 

Topics (Stage 2)

Further differentiation and applications Discrete random variables Integral calculus Logarithmic functions Continuous random variables and the normal distribution Sampling and confidence intervals.

 

Specialist Mathematics (Stage 2)

• Extends students’ mathematical experience in the areas of complex numbers and vectors. The study of functions, differential equations, and dynamic systems provides opportunities to analyse the consequences of more complex laws of interaction.
• Specialist Mathematics provides different scenarios for incorporating mathematical arguments, proofs, and problem-solving.

 

Topics (Stage 2)

Mathematical induction Complex numbers Functions and sketching graphs Vectors in three dimensions Integration techniques and applications Rates of change and differential equations.

Mathematics A

• Maths A is suitable for students who either struggled with mathematics in Year 10, or who do not require a knowledge of abstract mathematics in the future.
• There are fewer algebraic concepts in this subject, which is designed to help students develop an appreciation of the value of Mathematics and how mathematical concepts may be applied to a variety of life situations.
• The Mathematics A course is divided into four semesters.

 

Semester 1 (Year 11)	Semester 2 (Year 11)	Semester 3 (Year 12)	Semester 4 (Year 12)
Data Analysis Managing Money Applied Geometry Linking 2 and 3 Dimensions	Land Measurement Applied Geometry Statistics Managing Money	Managing Money Land Measurement Data Analysis Operations Research	Statistics Land Measurement Navigation, & An elective topic on Data

Mathematics B

• Maths B is considerably more theoretical than Maths A, requiring advanced algebra skills to successfully complete.
• Maths B is a pre-requisite for any tertiary course which deals with or uses math and/or science.
• In some schools, Maths B can be studied at the same time as either Maths A or Maths C, but not both.
• The course is divided into four semesters.

 

Semester 1 (Year 11)	Semester 2 (Year 11)	Semester 3 (Year 12)	Semester 4 (Year 12)
Functions (Linear, Quadratic, Absolute Value) Periodic Functions (Trigonometry, Sin/Cosine Functions) Applied Statistics (Mean, Median, Mode, Lie Factor) Applied Statistics 2 (Linear/Quadratic Regression, Residual Plots)	Exploring Data / Statistics Indices and Logarithms/ Exponential Functions Limits and Differential Calculus 1	Exponential and Log Functions Optimization Using Derivatives Integration Integral Calculus	Applied Statistical Analysis Integration Differential Calculus 2 Optimisation (Other Methods)

 

Mathematics C

• Maths C extends the topics taught in Maths B, and covers additional pure-maths topics (including complex numbers, matrices, vectors, further calculus and number theory).
• Maths C must be studied in conjunction with Maths B.
• Maths C can be a pre-requisite to tertiary courses with a heavy maths/science basis.
• The course is divided into four semesters.

 

Semester 1 (Year 11)	Semester 2 (Year 11)	Semester 3 (Year 12)	Semester 4 (Year 12)
Real and Complex Numbers Matrices Vectors Groups Structures & Patterns	Applications of Matrices Vectors Real and Complex Numbers Dynamics Structures and Patterns	Structures and Patterns Real and Complex Numbers Matrices Periodic Functions Calculus Option I & II	Vectors Calculus Dynamics Vectors Option I & II

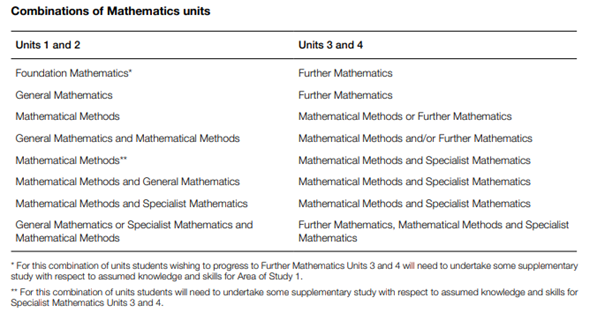
Foundation Mathematics

• Focuses on very basic practical maths skills and only runs at a Unit 1 + 2 level.
• These students generally would not undertake Unit 3 and 4 studies in VCE Mathematics.

Areas of Study

1. Space, shape and design
2. Patterns and number
3. Data
4. Measurement

 

General Mathematics

• General Mathematics Units 1 and 2 provide for a range of courses of study involving non-calculus based topics for a broad range of students
• They incorporate topics that provide preparation for various combinations of studies at Units 3 and 4 and cover assumed knowledge and skills for those units.

Areas of Study

1. Algebra and structure
2. Arithmetic and number
   1. Computation and practical arithmetic
   2. Financial arithmetic
3. Discrete mathematics
   1. Matrices
   2. Graphs and networks
   3. Number patterns and recursion
4. Geometry, measurement and trigonometry
   1. Shape and measurement
   2. Applications of trigonometry
5. Graphs of linear and non-linear relationships
   1. Linear graphs and models
   2. Inequalities and linear programming
   3. Variation
6. Statistics
   1. Investigating and comparing data distributions
   2. Investigating relationships between two numerical variables

 

Further Mathematics

• Further Mathematics Units 3 and 4 are designed to be widely accessible and is considered to be the second-least demanding of the four maths subjects taken by Victorian students.
• They provide general preparation for employment or further study, in particular where data analysis, recursion and number patterns are important.
• Further Mathematics consists of two areas of study, a compulsory Core area of study to be completed in Unit 3 and an Applications area of study to be completed in Unit 4.

Areas of Study – Unit 3

1. Data analysis
   1. Investigating data distributions
   2. Investigating associations between two variables
   3. Investigating and modelling linear associations
   4. Investigating and modelling time series data
2. Recursion and financial modelling
   1. Depreciation of assets
   2. Compound interest investments and loans
   3. Reducing balance loans
   4. Annuities and petpetuities
   5. Compound interest investment with periodic and equal additions

 

Mathematical Methods

• Mathematical Methods is the most common non-compulsory prerequisite for tertiary study in Victoria.
• Mathematical Methods Units 1 and 2 provide an introductory study of simple elementary functions, algebra, calculus, probability and statistics and their applications.
• Mathematical Methods Units 3 and 4 extend the study of simple elementary functions to include combinations of these functions, algebra, calculus, probability and statistics.

	Unit 1	Unit 2	Unit 3	Unit 4
Functions and graphs Algebra Calculus		Functions and graphs Algebra Calculus Probability and statistics	Functions and graphs Algebra Calculus Probability and statistics	Functions and graphs Algebra Calculus Probability and statistics

Specialist Mathematics (Units 1 and 2)

• Specialist Mathematics is considered the most advanced high school mathematics subject in Victoria.
• Specialist Mathematics integrates already learnt concepts of calculus into other fields of mathematics, thus giving Specialist Mathematics a far more practical orientation than standard mathematical subjects.
• Specialist Mathematics Units 1 and 2 incorporate topics that, in conjunction with Mathematical Methods Units 1 and 2, provide preparation for Specialist Mathematics Units 3 and 4 and cover assumed knowledge and skills for those units.

 

Areas of Study – Prescribed

2. Arithmetic and number
   1. Number systems and recursion
3. Geometry, measurement and trigonometry
   1. Geometry in the plane and proof
   2. Vectors in the plane
4. Graphs of linear and non-linear relations
   1. Graphs of non-linear relations

 

Areas of Study – Optional

1. Algebra and structure
   1. Logic and algebra
   2. Transformations, trigonometry and matrices
2. Arithmetic and number
   1. Principles of counting
3. Discrete mathematics
   1. Graph theory
4. Graphs of linear and non-linear relations
   1. Kinematics
5. Statistics
   1. Simulation, sampling and sampling distributions

 

Specialist Mathematics (Units 3 and 4)

• Specialist Mathematics Units 3 and 4 are designed to be taken in conjunction with or following completion of Mathematical Methods Units 3 and 4.
• The areas of study extend content from Mathematical Methods Units 3 and 4 to include rational and other quotient functions as well as other advanced mathematics topics such as complex numbers, vectors, differential equations, mechanics and statistical inference.

 

Areas of Study – Prescribed

1. Functions and graphs
2. Algebra
   1. Rational functions
   2. Complex numbers
3. Calculus
   1. Differential and integral calculus
   2. Differential equations
   3. Kinematics: rectilinear motion
4. Vectors
   1. Vectors
   2. Vector calculus
5. Mechanics
6. Probability and statistics
   1. Linear combinations of random variables
   2. Sample means
   3. Confidence intervals for means
   4. Hypothesis testing

 

Sources:

• https://www.vcaa.vic.edu.au/Documents/vce/mathematics/2016MathematicsSD.pdf
• https://www.vcaa.vic.edu.au/curriculum/vce/vce-study-designs/Pages/vce-study-designs.aspx

Mathematics Specialist

• Based on AC: Specialist Mathematics.
• Should be studied in conjunction with the Mathematics Methods course, on which it builds.

Mathematics Methods

• Based on AC: Mathematical Methods.
• May be studied in conjunction with the Mathematics Specialist course.

Mathematics Applications

• Based on AC: General Mathematics.

Mathematics Essential

• Based on AC: Essential Mathematics.
• Focuses on using mathematics effectively, efficiently and critically to make informed decisions.

Unit 1	Unit 2	Unit 3	Unit 4
Basic calculations, percentages and rates Using formulas for practical purposes Measurement Graphs	Representing and comparing data Percentages Rates and ratios Time and motion	Measurement Scales, plans and models Graphs in practical situations Data collection	Probability and relative frequencies Earth geometry and time zones Loans and compound interest

Mathematics Foundation

• Focuses on building the capacity, confidence and disposition to use mathematics to meet the numeracy standard for the WACE.
• It provides students with the knowledge, skills and understanding to solve problems across a range of contexts including personal, community and workplace/employment.

Unit 1	Unit 2	Unit 3	Unit 4
1.1:    Whole numbers and money 1.2:    Addition and subtraction with whole numbers and money 1.3:    Length, mass and capacity 1.4:    Time 1.5:    Data, graphs and tables	2.1:   Understanding fractions and decimals 2.2:    Multiplication and division with whole numbers and money 2.3:    Metric relationships 2.4:   Perimeter, area and volume 2.5:   The probability of everyday events	3.1: The four operations: whole numbers and money 3.2: Percentages linked with fractions and decimals 3.3: The four operations: fractions and decimals 3.4: Location, time and temperature 3.5: Space and design	4.1: Rates and ratios 4.2: Statistics and probability 4.3: Application of the Mathematical Thinking Process

 

Mathematics Preliminary

• Focuses on the practical application of knowledge, skills and understandings to a range of environments that will be accessed by students with special education needs.

1        Whole number

2        Addition and subtraction of whole numbers

3.       Money

4.       Addition and subtraction of money

5.       Multiplication and division

6.       Multiplication and division of money

7.       Time

8.       Measurement

9.       Location

10.    Shape and transformation

11.    Chance and data

 

Sources:

• https://senior-secondary.scsa.wa.edu.au/syllabus-and-support-materials/mathematics
• Australian Curriculum, Assessment and Reporting Authority. (2020). Overview of the senior secondary Australian Curriculum. Retrieved from https://www.australiancurriculum.edu.au/senior-secondary-curriculum/mathematics/overview-of-the-senior-secondary-australian-curriculum/